Perspektive als Wahrnehmungskonvention?

Perspektive als Wahnehmungskonvention: 3D-Grafiken mit Parallelprojektion, Isometrie und Zentralperspektive (Grafik: Martin Dühning)

Gibt es so etwas wie eine objektive Perspektive? Oder handelt es sich bei Perspektiven nur um subjektive Konstruktionen? Ist Perspektive vielleicht gar nur eine gesellschaftliche Konvention?

1. Objektive Standpunkte oder reine Subjektivität?

Man erwartet von einer wissenschaftlichen Abhandlung – und sei sie noch so klein? Größtmögliche Objektivität! Frei von allen die Realität der Sache verzerrenden subjektiven Ansichten und Blickwinkeln soll der fokussierte Gegenstand, das Thema, untersucht, diskutiert und schließlich objektiv durchdrungen werden. Am Ende steht idealerweise ein möglichst realitätsgerechtes tieferes Verständnis des behandelten Gegenstandes. Die persönliche Perspektive des Wissenschaftlers wird dabei besonders kritisch beäugt. Da man wohl leider nicht umhin kommt, sie als vorhanden hinnehmen zu müssen, muss man doch zumindest versuchen, sie durch bestimmte Techniken der Wahrheitsfindung irgendwie zu neutralisieren. Sofern man schon diesen Versuch ablehnt, kann man für seine Untersuchungen keinerlei Objektivität postulieren; solange man perspektivisch bleibt, kommt man an die Gegenstände nicht wahrheitsgemäß heran.

Paradoxer Weise wird der Perspektive in der Kunst genau die entgegengesetzte Bedeutung zugesprochen. Hier gilt als Allgemeinplatz: Ein Bild gibt die Realität genau dann am naturgetreuesten wieder, wenn es perspektivisch einwandfrei, aber eben perspektivisch, und zwar äußerst perspektivisch, gemalt oder gezeichnet wurde. Lässt man nämlich die Perspektive in einem Bild weg, wird es die dargestellten Gegenstände falsch oder bestenfalls verzerrt darstellen. Man kommt also in diesem Falle nur an die Gegenstände heran, indem man sich der Perspektive hingibt.

Diesen Widerspruch könnte man höchstens dadurch entkräften, indem man davon ausgeht, dass „Perspektive“ in beiden Fällen jeweils etwas anderes meint. Oder aber, was besonders beliebt bei Philosophen und Sprachwissenschaftlern ist, man verteufelt die visuellen Medien per se, und spricht ihnen jeden Objektbezug ab, eben weil sie perspektivisch sind. Ein weiterer möglicher Einwand wäre: Perspektive unterscheide sich in Kunst und Wissenschaft, weil beide grundverschiedene Zielsetzungen hätten. Der Wissenschaft gehe es um das handfeste Objekt, Kunst dagegen beabsichtige Ästhetik. – Dieser Einwand ist jedoch nur sehr bedingt tragfähig. Er geht einerseits von einer unfehlbar-objektiven Wissenschaft aus, andererseits leugnet er den Erkenntnisgehalt von ästhetischer Vermittlung. Medientheoretisch gesehen haben wir es ohnehin immer mit Medien zu tun, welche Informationen mit integriertem Wahrheitsanspruch vermitteln, unabhängig davon, ob es sich um das Medium Sprache, Schrift, Bild oder eine Kombination davon handelt. Im Einzelnen ist es übrigens auch äußerst schwierig, Kunst und Wissenschaft medial zu trennen.

Daher möchte ich mich nicht den klassisch-dualistischen Apologien für oder gegen Bildkunst anschließen. Vielmehr möchte ich aber mit Nelson Goodman und Erwin Panofsky untersuchen, inwiefern es sich bei der Perspektive in der Kunst wirklich um eine Strategie zur objektiven Wahrheitsvermittlung handelt, oder ob es sich doch nicht vielmehr um eine „Wahrnehmungskonvention“ handelt. Dazu möchte ich zuerst allerdings meine eigene durchaus subjektive Perspektive zu diesem Thema erläutern, um zu erklären, worum es eigentlich geht.

2. Ein kleiner Expertenstreit

In der einstigen Klasse 10a des Klettgaugymnasiums Tiengen kam es ihm Herbst 1990 zu einem unbedeutenden und kleinen Streit zwischen dem damaligen Mathelehrer und dem Kunsterzieher. Dennoch wurde er von uns Schülern mit größter Freude und Aufmerksamkeit verfolgt. Schließlich konnte man hier jeweils den einen Lehrer mit der Autorität des jeweils anderen matt setzen – eine Chance, die von 27 Schülern in einem gewissen Alter dankbar genutzt wurde. Worum es den meisten Schülern ging, war einmal mehr, eine Lehrkraft ungestraft aufziehen zu können. Aber worum ging es den Lehrern?

Es begann alles mit der Perspektivenlehre. Dort brachte uns unser Kunstlehrer bei, wie wir einen Würfel richtig und naturgetreu konstruieren müssen. Da gab es mehrere Möglichkeiten, wie wir erfuhren, die meisten hatten aber den einen und den anderen Fehler. Was aber jedenfalls ganz wichtig sei, wäre, dass man die horizontale Grundkante eines Objektes nie parallel zur unteren Bildkante zeichnen dürfe. Dies sei in jedem Fall unnatürlich; und dass es tatsächlich auch so ist, könne man jedem Foto entnehmen. Wenn ich mich noch recht entsinne, bot uns unser Kunsterzieher sogar ein Prämie dafür an, wenn es uns gelänge, ein Foto zu machen, was das Gegenteil bewiesen hätte. Wie man sich vielleicht denken kann, erhielt niemand eine solche; und zwar deshalb, weil es niemandem gelang.

Etwa zur gleichen Zeit behandelten wir in Mathematik Darstellende Geometrie. Wieder wurde ein Würfel an die Tafel gezeichnet, aber diesmal einer mit mathematisch-objektiven Zahlen daran, und außerdem mit einer horizontalen Grundkante, die parallel zur unteren Tafelkante war. Dies erregte in der Klasse allgemeinen Aufruhr. 27 junge Kunstexperten wiesen den Mathelehrer darauf hin, dass die Darstellung des Würfel falsch sei. Dieser überprüfte seine Berechnungen mehrmals, kam aber immer wieder zum selben Ergebnis. Auch der Hinweis darauf, dass man niemals die untere Linie eines Körpers parallel zur Bildkante zeichnen dürfte, verstand er wohl nicht. Er habe Würfel schon immer so gezeichnet. Das Argument, dass dies aber so nicht naturgetreu wäre, verstand er nicht. Schließlich und endlich komme es ihm sowieso nur darauf an, geometrische Sachverhalte anschaulich darzustellen.

Wir erzählten dies natürlich sofort unserem Kunsterzieher. Dieser sah sich dadurch einmal mehr darin bestätigt, wie sehr die meisten Menschen doch in Sehkonventionen verhaftet seien: Weil man einfach gewohnt sei, etwas so oder so zu zeichnen, sehe man es schließlich auch so. Gerade die Perspektivenlehre werde von den meisten Menschen daher anfang nicht richtig verstanden. Kunst an sich erfordere aber ein kritisches und offenes Sehen: Man müsse lernen, die Dinge zusehen, wie sie sind, und nicht als das, für was man sie hält.

Der daraufhin folgende Streit zwischen unserem Kunsterzieher und unserem Mathelehrer endete – wie so oft, darin, dass sich jeder auf seinem apologetischen Posten verschanzte, und sein Recht behielt. Die meisten von uns Schülern glaubten aber damals eher unserem Kunsterzieher, weil er uns nicht nur mit Worten und Gleichungen, sondern auch mit handfesten Fotos beweisen konnte, was er meinte. Ich glaubte ihm daher solange, bis ich Nelson Goodmans „Sprachen der Kunst“ kennenlernte. Dann kamen mir erstmals begründete Zweifel, was die Objektivität auch dieser Form von Perspektive angeht.

3. Nelson Goodmans Kritik an der Zentralperspektive

Im Rahmen seiner Symboltheorie kommt Nelson Goodman in seinem 1998 erschienenen Buch „Sprachen der Kunst, Entwurf einer Symboltheorie“ auf S. 21 auch auf die Perspektive zu sprechen. Für ihn ist sie allerdings letztlich nichts anderes als ein weiteres Beispiel für eine verabsolutierte Konvention. Sofern man in der Perspektive eine Möglichkeit sieht, Realwelt naturgetreu auf Fläche darzustellen, wäre sie sonst auch ein Gegenargument gegen Goodmans These, dass Bilder Repräsentationen sind, statt Kopien von Realität, und dass Repräsentation auf einem konventionalisierten Symbolsystem basiert, nicht aber etwa auf Ähnlichkeit. Ziel von Goodmans Behandlung der Perspektive ist daher nicht vordergründig, zu zeigen, was Perspektive ist und was sie leistet, sondern, was Perspektive gerade nicht ist und was sie nicht leisten kann – und zwar ist Perspektive nach Goodman kein Mittel, Raum nach dem Prinzip der Ähnlichkeit auf Fläche zu übertragen. Statt dessen handelt es sich bei den Gesetzen der klassischen Perspektive laut Goodman um ein konventionalisiertes Regelschema, ein grafisches System zur Repräsentation von Räumlichkeit. Für diese auf den ersten Blick doch ungewohnte These führt Goodman folgende Argumente an:

Die klassische Zentralperspektive geht von einem einzigen unbeweglichen Auge aus, das ein Bild nur von einem vorbestimmten Blickwinkel aus, auf einen ganz bestimmten Punkt hin (den Fluchtpunkt) betrachtet; denn nur unter diesen Bedingungen stimmt die Perspektive (im Idealfall) genau mit der Realität überein. Die Regeln der klassischen Perspektive widersprechen damit der menschlichen Wahrnehmungserfahrung, da das menschliche Auge ständig abtastet und niemals nur starr und einäugig fokusiert (vgl. Goodman, S. 23).
Die Regeln der klassischen Perspektive widersprechen der tatsächlichen Wahrnehmung aber auch darin, dass ihnen gemäß in der Zeichnung nur die Vertikalen der Bildebene (wie z. B. Eisenbahnschienen) zum Fluchtpunkt hin konvergieren, aufrechte Vertikalen (wie z. B. Telegraphenmasten) aber parallel gezeichnet werden müssen. Gemäß der tatsächlichen menschlichen Wahrnehmung müssten aber auch letztere konvergieren.
Daher, so folgert Goodman, könne man nicht davon sprechen, dass die Perspektive ein Mittel zur naturgetreuen Kopie visueller Raumwahrnehmung auf Fläche sei. Dazu zeige sie zu viele Schwächen auf.
Von dieser Argumentation, die auf Unzulänglichkeiten des perspektivischen Darstellungsverfahrens rekurriert, ist jedoch noch Goodmans abschließende Ablehnung der Perspektive an sich zu unterscheiden: „das Verhalten des Lichts sanktioniert weder unsere gewohnte noch irgendeine andere Weise der Wiedergabe des Raumes; und die Perspektive stellt keinen absoluten oder unabhängigen Treuestandard zur Verfügung“ (vgl. Goodman, S. 29). Hier wird also nicht die Perspektive, sondern gleich die Optik selbst als Basis von Repräsentation abgelehnt: Nach Goodmans Auffassung spielt optische Ähnlichkeit keine sanktionierende Rolle bei der Repräsentation.

Es ist zu klären, wie solche Behauptungen aufrecht erhalten werden können. Dazu werden wir wohl nicht darum herum kommen, zumindest oberflächlich zu beleuchten, wie Raum technisch auf Fläche repräsentiert oder abgebildet wird.

4. Unterschiedliche grafische Systeme zur Repräsentation von Räumlichkeit

4.1 Stapelung und Hintansetzung bzw. Verjüngung

Es gibt verschiedene Möglichkeiten, die Perspektivenlehre anzugehen. Man kann sie historisch oder kunsthistorisch oder aber auch von ihrer Komplexität her aufrollen. Erwin Panofsky wählte seinerzeit den kunsthistorischen Weg, was ja für ihn als Kunsthistoriker auch nahelag. Ich möchte hier verschiedenen Ansätze von konstruierter Räumlichkeit aber von ihrer Konstruktion her behandeln. Historische Einordnungen werden dabei kaum eine Rolle spielen, wenn gleich sie auch äußerst aufschlußreich wären.

In diesem Sinne beginne ich auch mit Darstellungsmethoden, die von der Bildenden Kunst selbst selten als „Perspektive“ akzeptiert wird, aber doch zumindest eine Vorstufe davon ist: Die erste davon wäre die Stapelung von Bildobjekten übereinander. In ihrer einfachsten Form bedeutet das, einzelne Gegenstände übereinander abzubilden, wobei oben immer auch gleich „weiter hinten“ im Bild bedeuten soll. Schon bei dieser einfachen Form der Repräsentation von Raum auf Fläche könnte man sich fragen, inwiefern Goodmans Kritik hier greift. Wäre denn hier auch eine „umgekehrte Perspektive“, quasi also „unten gleich hinten“ denkbar? Dies erscheint dem Betrachter doch irgendwie unausgegoren. Selbst wenn man versucht, eine solche Darstellung durch zusätzliche Hinweise, wie die Verjüngung der hinten gelegenen Gegenstände betont, ergibt sich kaum der Eindruck, das unten hinten darstellen soll. Zumindest nicht, solange die Objekte auf einer Ebene stehen sollen, und nicht von einer Decke herunter hängen (wie beispielsweise Lampen oder Fledermäuse).

Zugegeben, es wäre möglich, einen Betrachter mit Mühe daraufhin zu schulen, unten als hinten zu deuten. Allerdings liegt es dem „ungeschulten“ Auge trotzdem viel näher, oben als hinten zu deuten. Selbst Zeichnungen von Kindern verfahren in der Regel nach diesem System. Liegt bei dieser Raumrepräsentation also nicht doch optische Ähnlichkeit mit unserer Raumwahrnehmung zugrunde?

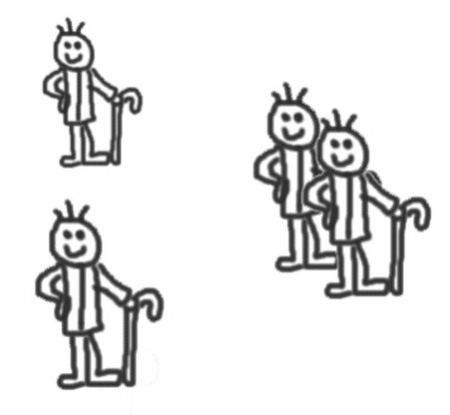
Links einfache Übereinandersetzung (kombiniert mit Verjüngung), rechts Hintansetzung (Grafik: Martin Dühning)

Eine weitere, schon etwas anspruchsvollere Methode zur Darstellung von Räumlichkeit ist die Hintansetzung. Hier werden die Objekte im Bild nicht nur übereinander plaziert, sondern auch „hintereinander“, was dadurch berücksichtigt wird, dass sich die einzelnen Objekte dabei überschneiden. Dieses Verfahren stellt gegenüber dem bloßen Übereinandersetzen von Gegenständen schon eine wesentlich abstraktere Darstellungsstufe dar: Man beachte nämlich, dass hier Gegenstände voneinander visuell subtrahiert, beziehungsweise addiert werden. Dies muss ersteinmal „begriffen“ werden. Wenn sich beispielsweise zwei Strichmännchen überlappen und daher ein Arm des hinteren Strichmännchens nicht zu sehen ist, bedeutet das ja nicht, dass dieser Arm als fehlend zu denken ist – auch wenn er visuell nicht abgebildet wurde. Das Ganze soll vielmehr anzeigen, dass der Arm, den man nicht sieht, deshalb nicht dargestellt ist, weil er von einem anderen Gegenstand als überdeckt gedacht werden soll.

Auch diese Methodik ist wohl eher aufgrund der natürlichen Sehwahrnehmung entstanden. Logisch macht eine derartige „Begriffsarithmetik“ nämlich kaum einen Sinn, sondern böte eher Raum für Missverständnisse. Eine Darstellungspraxis, die es allein auf Repräsentation und nicht auch auf Mimese der Alltagserfahrung abgesehen hat, wird solche Missverständnisse aber eher vermeiden wollen, um die repräsentierte Information nicht zu gefährden. Das Überschneiden von Gegenständen in Bildern ist wohl doch eher ein Zugeständnis an die natürliche Wahrnehmung, als ein willkürlich entstandener repräsentativer Akt. Ähnliches gilt wohl auch für die Verjüngung, also dass Gegenstände desto kleiner abgebildet werden, je weiter hinten im fiktiven Raum des Bildes sie lokalisiert werden sollen. Auch sie führt in ihrer Anwendung eher zur Verwirrung. Dass man die Verjüngung umkehren könnte, ohne „Scheinriesen“ produzieren, die dem Betrachter in die Ferne hin immer größer erscheinen, scheint fast ausgeschlossen.

Die Verwendung von Strichmännchen ist zugegeben relativ tückisch. Zwar sind sie sehr einfach zu zeichnen, aber bei weitem nicht so einfach zu denken. Die wenigstens Strichmännchen z. B. auf Kinderbildern, sind so simpel wie sie daherkommen: Was ihnen an Ähnlichkeit fehlt, müssen sie zwangsläufig nämlich durch Abstraktion ausgleichen. Daher sind „Kritzeleien“ für Außenstehende oft auch nur schwer durchdringbar. Eben weil Strichmännchen aber vorangig repräsentativ sind, habe ich sie hier als Beispiel verwendet. Je abstrakter nämlich Darstellungen sind, desto deutlicher fällt ins Auge, wo sie doch „ähnlich“ sind.

Stapelung, Hintansetzung und Verjüngung sind seit jeher Mittel zur einfachen Repräsentation von Räumlichkeit. Was ihnen allerdings fehlt, ist ein spezielleres Regelsystem, mittels dessen sie unzweideutig eingesetzt werden können: Um wieviel höher muss ich Würfel B gegenüber Würfel A plazieren, wenn dieser sich beispielsweise drei Meter weiter hinten befindet? Um wieviel kleiner muss Würfel B dargestellt werden? Wie müssen sich beide gegebenenfalls überschneiden? – Diese Fragen sind hier noch unsystematisiert, für den Zeichner aber gleichermaßen wichtig wie für den Betrachter zum Verständnis des späteren Bildes.

4.2 Parallelprojektion

Das einfachste System linearer Darstellung von Räumlichkeit ist wohl die Parallelprojektion. Sie stellt insofern eine Besonderheit dar, als dass sie schon von ihrer Konzeption eher auf eine einfache aber anschauliche Repräsentation von geometrischen Räumen aus ist, als auf wirklichkeitsgetreue Abbildung. Ziel der Parallelprojektion ist es, geometrische Sachverhalte so einfach wie möglich geometrisch korrekt zu repräsentieren. Geometrie ist hierbei wieder einmal mehr von der natürlichen optischen Wahrnehmung zu unterscheiden. Zwar wird hier Raum dargestellt, aber ein logisch-mathematischer Raum, kein Erfahrungsraum und erst recht nicht die Realität, wie das menschliche Auge sie wahrnimmt.

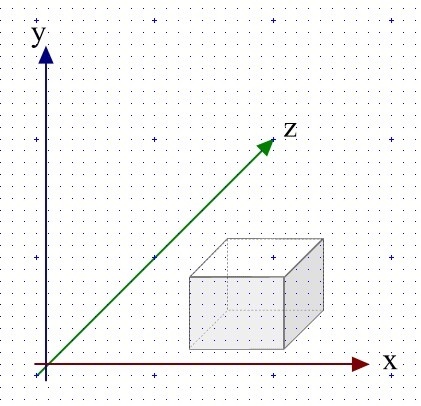
Parallelprojektion eines Quaders (Grafik: Martin Dühning)

Das Konstruktionsprinzip der Parallelprojektion ist recht einfach: Man zeichnet zuerst die Frontalfläche des Objektes in ein zweidimensionales Koordinatensystem, für einen Quader also beispielsweise ein Rechteck. Dann extrudiert man die Grundfläche, indem man dasselbe Rechteck versetzt nach rechts oben abträgt. Dadurch entstehen erst einmal zwei Flächen, die sich gemäß des Prinzips der Staffelung überschneiden. Das besondere an der Parallelprojektion ist nun aber, dass es sich hierbei um keine willkürliche Staffelung, sondern eine wirklich eindeutige Konstruktion handelt: Die Position der Hintergrundfläche ergibt sich nämlich eindeutig aus der „Tiefe“ des darzustellenden Körpers, sodass sich sämtliche Punkte der Vordergrundfläche mittels evidenter linearer oder trigonometrischer Gleichungen entlang einer diagonalen Z-Achse eindeutig auf die Fläche abtragen lassen. Die Evidenz besteht dabei im festgelegten Gleichungssystem, dass die räumlichen Koordinaten auf die Fläche projiziert. Dies manifestiert sich grafisch in der Steigung der gedachten Tiefenachse (der Z-Achse), und ihrer Eichung im Verhältnis zu den beiden real vorhandenen Flächenachsen (X- und Y-Achse). In der Regel verwendet man für die Z-Achse die lineare Gleichung Y=X+1, erhält also die Z-Achse als interpolierte Gerade im Winkel von 45° gegenüber X- und Y-Achse. Dieses Verfahren ist besonders praktisch, weil man für die Konstruktion daher einfach die „Kästchen“ des Karopapieres verwenden kann. Auf ähnliche Weise lassen sich auch komplexe und unregelmäßige Körper mathematisch eindeutig darstellen, indem man sie in dem dadurch entstehenden kubischen Koordinatensystem lokalisiert.

Aller Eindeutigkeit dieses Repräsentationssystems zum Trotz wird man doch einwenden müssen, dass diese Art der Raumdarstellung – so mathematisch genau und korrekt sie auch sein mag – bisweilen deutlich unrealistisch wirkt, da Objekte hier immer noch stur nebeneinander gestaffelt werden, und sie sich in die Ferne hin noch nicht einmal verkürzen. Störend wirkt vor allem, dass alle Objekte parallel zum Betrachter konzipiert sind, unabhängig von ihrer Lage im Raum. Dies mag bei einzelnen komplexen geometrischen Gebilden nicht so sehr ins Auge fallen. Aber je einfacher die dargestellten Körper sind, und je mehr nebeneinander gezeichnet werden, desto verzerrter wirken sie zusammen.

Woran das liegt, ist natürlich eine gerade im Hinblick auf Goodmans These eine interessante Frage. Sobald man nämlich hier wieder damit argumentiert, die Parallelprojektion wirke daher unrealistisch, weil sie gegen die menschliche Wahrnehmungsgewohnheit verstößt, so muss man auch in diesem Falle der Bedeutung von Ähnlichkeit des Abgebildeten mit der Realität hier einen weiteren Vorrang vor der Konventionalität einräumen. Denn das mathematisch-geometrische Weltbild und seine diesbezügliche Emanation, die Parallelprojektion, sind inzwischen hochkonventionell und geradezu Allgemeingut. Gemäß Goodmans These müsste daher die Parallelprojektion für uns inzwischen auch viel realistischer wirken als die Zentralperspektive, da sie in den Wissenschaften und im öffentlichen Diskurs faktisch viel häufiger eingesetzt wird und damit gewohnter ist als alle anderen Arten von Raumkonstruktionen. Von der Quantität des Auftretens scheint allerdings hier der Realismus anderer Perspektivkonstruktionen nicht betroffen zu sein: Zentralperspektivische und vor allem neuere Mehrfluchtpunkt-basierte Darstellungen wirken unverändert wesentlich realistischer.

4.3 Zentralperspektive

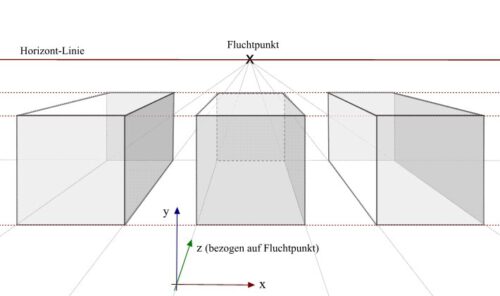
Die Zentralperspektive ist wohl die älteste konsequent geometrische Perspektive. Sie wurde bereits zu Beginn der Neuzeit, also in der Renaissance, entwickelt. In gewisser Weise stellt sie dennoch von der Konzeption her schon eine Erweiterung der Parallelprojektion dar. Auch hier geht man nämlich letztendlich von Objektflächen aus, die auf der Bildfläche gemäß geometrischer Gesetze zu Körpern extrudiert werden. Im Unterschied zur dezentralen Parallelprojektion, bei der alle Körper lediglich durch lineare Verschiebung entstehen, werden die Körper bei der Zentralperspektive aber auf einen bestimmten Punkt hin, den Fluchtpunkt, konstruiert. Somit haben wir es nicht mehr mit einem kubischen Raum, sondern einer Pyramide zu tun. Dadurch macht es die Zentralperspektive möglich, Körper in die Tiefe hin zu verkürzen.

Darstellung von drei Quadern mittels der Zentralperspektive. „Korrekt“ erscheint bei dieser Darstellungsmethode nur der mittlere Quader, weil er dem Fluchtpunkt sehr nahe ist. Die beiden äußeren Quader dagegen erscheinen unnatürlich. Die unnatürlichen Verzerrungseffekte nehmen in dem Maße zu, wie sich die Objekte vom Fluchtpunkt entfernen. (Grafik: Martin Dühning)

Die eigentliche Besonderheit der Zentralprojektion – und sofern für Goodmans Argumentation wichtig – besteht aber wohl vor allem in ihrem Anspruch, Realität (und nicht etwa nur Geometrie) in Fläche abbilden zu können. Dieser Anspruch zeigt sich auch in ihrer berühmten Zeichenhilfe, dem Netzrahmen. Dabei handelt es sich um einen Rahmen, der mit einem Netz von Fäden bespannt ist, und durch den der Zeichner blickt, und reale Objekte, oder Landschaft, auf Fläche projiziert, diese in Flächen-Koordinaten umdenkt und dann auf seine Zeichenfläche überträgt. Dabei geht man von der Vermutung aus, dass auch das menschliche Auge (bzw. die Netzhaut) eine innere Fläche aufweist, auf welche die Lichtstrahlen des Raumes im Sinne einer „Sehstrahlenpyramide“ projiziert werden.

Diese Vermutung, so schön und praktisch sie für eine Handhabung in Kunst und darstellender Wissenschaft auch wäre, ist allerdings falsch, da die Netzhaut keine ebene, rechteckige Fläche darstellt. Daher kann Goodman zurecht darauf hinweisen, dass die Zentralperspektive ihrem Anspruch auf Realitätstreue nur unzureichend gerecht wird, weil sie beispielsweise alle Parallelen der Y-Achse nicht konvergieren lässt. Der von Goodman eingebrachte Vorschlag, die Schienen in ihrer Funktion als als Tiefenlinien parallel zu zeichnen ist aber insofern unlogisch, als dass diese zwangsläufig in jedem Fall auf den Fluchtpunkt hin konvergieren müssen. Selbst nach dem Modell der Sehstrahlenpyramide ist es übrigens nicht ausgeschlossen, diese Linien konvergieren zu lassen, und stattdessen die Tiefenlinien der Ebene parallel zu zeichnen: Insofern man den Fluchtpunkt zuvor in die Höhe verlegt (also praktisch eine Ansicht von unten nach oben), kann man so durchaus auch Telegraphenmasten konvergieren lassen – die Schienen dann allerdings nicht mehr, da sie dann nicht mehr auf den Fluchtpunkt zu beziehen wären. Das Problem der klassischen Zentralperspektive liegt nämlich darin, dass hier nur ein Fluchtpunkt vorhanden ist, aber mindestens zwei nötig wären, um beide Linien konvergieren zu lassen. Ebenso ist, über Goodman hinaus, bei der klassischen Zentralperspektive kritisch zu bemerken, dass hier wie bei der Parallelprojektion alle Grundkanten der Flächen parallel zur Grundkante der Bilder verlaufen. Dies verursacht wie bei der Parallelprojektion einen unerwünschten Verzerrungseffekt für alle Objekte, deren Position auf der X-Achse zu weit vom Fluchtpunkt entfernt liegt.

Im Unterschied zur Parallelprojektion fällt das bei der Zentralperspektive aber nur dann ins Gewicht, wenn man seine Blicke von der vorgegebenen Blickrichtung des Bildes, dem Fluchtpunkt, abwendet, und quasi „widerrechtlich“ die Objekte am Rand betrachtet; oder anders herum gesagt, um Goodmans Argument wieder aufzugreifen: Das zentralperspektivisch konstruierte Bild erscheint in seiner Perspektive nur dann naturgetreu, wenn man es mit einem Auge durch ein Guckloch hindurch, sowie fokussiert auf seinen Fluchtpunkt hin betrachtet. Andernfalls ist die Illusion dahin, weil sich unnatürliche Verzerrungseffekte zu den Seiten hin ergeben. Diese fallen gerade deswegen störend auf, weil das Auge des Bildbetrachters im Normalfall gerade eben nicht auf den Fluchtpunkt fixiert ist.

4.4 Isometrie

Eine mögliche Methode, die marginalen Verzerrungseffekte zu mindern, besteht darin, die Objekte im Bild über Eck zu stellen, sie also so zu plazieren, dass ihre Grundkanten nicht parallel zu den horizontalen Bildkanten sind. Dabei ist es aber nicht damit getan, die Objekte einfach zu rotieren, da damit auch die Höhenachse (Y-Achse) verdreht würde. Vielmehr muss auch das ihnen zugrunde liegende kubische Raumkonzept selbst entsprechend verschoben werden.

Die in dieser Hinsicht einfachste Konstruktionsmethode ist die sogenannte Isometrie. Sie wird hauptsächlich von ästhetisch anspruchsvolleren Mathematikern (z. B. Architekten), aber auch beispielsweise in vielen einfachen 2D-Computer-Anwendungen eingesetzt, die einen etwas höheren Wert auf eine „natürlich“ wirkende Darstellung legen. Dazu zählen beispielsweise die meisten dreidimensionalen Graphen und Diagramme, aber auch viele Computerspiele, hier vor allem wieder Wirtschaftsimulationen und Strategiespiele wie SimCity oder Civilisation II, aber auch Hexagon-basierte Spiele wie Siedler 2 funktionieren letztlich nach den Regeln der Isometrie.

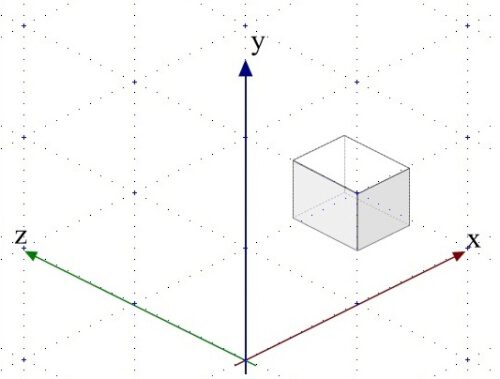
Isometrische Darstellung eines Quaders (Grafik: Martin Dühning)

Die Isometrie funktioniert ansonsten analog zur Parallelprojektion, basiert also ebenfalls auf geometrischen bzw. trigonometrischen Gleichungen, und nimmt auf Verkürzung in die Tiefe hin keine Rücksicht. Im Unterschied zur Parallelprojektion wird die X-Achse hier aber um 30° oder 45° entgegen des Uhrzeigersinns gedreht. (Nun gut, Der Winkel der X- bzw. Z-Achse gegenüber der Y-Achse kann fast beliebig variieren; wichtig ist nur, dass sie nicht rechtwinklig zur Höhenachse (Y-Achse) ist. Daraus resultieren mehrere mögliche Systeme der Isometrie. Die hier vorgestellte axonometrische Isometrie ist allerdings die gebräuchlichste). Die Y-Achse (Höhen-Achse) bleibt dabei aber unverändert parallel zu den vertikalen Bildkanten. Die Z-Achse ergibt sich aus einer Spiegelung der X-Achse an der Y-Achse. Bei der Grundriss-Isometrie oder der „einfachen“ Isometrie kann der Winkel zwischen Z- und Y-Achse aber auch anders gewählt werden. Der Winkel zwischen X- und Z-Achse sollte dabei aber 90° nicht unterschreiten, da die Darstellung sonst zu verzerrt erscheint (vgl. auch Birkhofer, S. 15).

Der Nachteil, der sich aus der Verschiebung des kubischen Koordinatensystems ergibt, ist in erster Linie, dass sich damit auch die mathematischen Gleichungen zur Übertragung der Punkte in die Fläche verkomplizieren. Es reicht bei der Isometrie daher auch oft nicht mehr aus, einfach Karos auf dem Papier abzuzählen, wie noch bei der Parallelprojektion. Dennoch wirken isometrische Darstellungen – obwohl sie noch nicht einmal räumliche Verkürzungen berücksichtigen, oft naturgetreuer als die Zentralperspektive.

Auch hier stellt sich wieder die Frage: warum? Wenn allein Gewohnheit und Konvention für Realismus maßgeblich wären, wäre auch hier die Parallelprojektion aufgrund ihrer Verbreitung klar im Vorteil. Sobald man aber als Grund angibt, dass die Isometrie der natürlichen Wahrnehmung insofern eher gerecht wird, als dass man in der Natur niemals drei Seiten eines Körpers gleichzeitig sehen oder fotografieren kann, solange dieser mit paralleler Grundkante zum Betrachter steht, argumentiert man schon wieder mit Ähnlichkeit und kann sich nicht mehr allein auf Konventionalität berufen.

Goodman dürfte dieser Fortschritt in Richtung optischer Treue aber immer noch kaum beeindrucken, da die Isometrie lediglich eine verbesserte Parallelprojektion darstellt. Solange man ihre Fortschritte mit der Fluchtung der Zentralperspektive verbindet, ist sie nicht „korrekt“; und ob das ohne weiteres gelingt, ist wieder eine andere Frage.

4.5 Perspektiven mit mehreren Fluchtpunkten

Versucht man nämlich Isometrie und Zentralperspektive in Einklang zu bringen, steht man nun vor der konzeptionell unlösbaren Schwierigkeit, dass man nun mit einem einzigen Fluchtpunkt nicht mehr auskommt. Stattdessen sind nun mindestens zwei nötig: einer für alle Vertikalen, die in Richtung der Z-Achse verlaufen – und einer für ihre Pendants in Richtung der X-Achse (welche zuvor parallel zur Bildkante war).

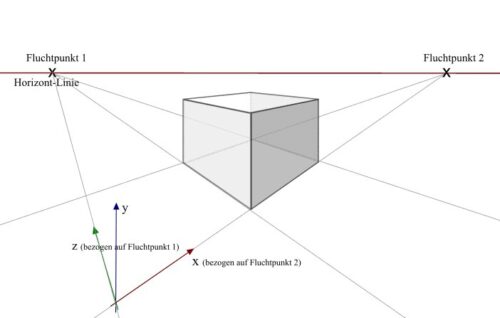
Übereckstellung eines Quaders mittels zweier Fluchtpunkte (Grafik: Martin Dühning)

Setzt man nun aber beispielsweise zwei Fluchtpunkte in das Bild, hat man nunmehr kein Zentrum mehr, sondern damit auch zwei Blickpunkte, was unter Umständen zu noch unrealistischeren Verzerrungen führen kann als bei der Zentralperspektive, vor allem zur Mitte des Bildes hin, also dort wo der (gedachte) Betrachter selbst steht.

Weshalb die bei zwei bzw. drei oder vier Fluchtpunkten auftretenden Verzerrungen allerdings „unrealistisch“ erscheinen, ist eine weitere interessante Frage. Optisch ist diese Darstellungsform gegenüber der Zentralperspektive nämlich um einiges adäquater. Vielleicht sind wir die Zentralperspektive inzwischen wirklich derart gewohnt, dass wir sie für realistischer halten als die eigentliche optische Realität. In diese Richtung zielt ja auch Goodmans Hinweis auf Korrekturlinsen bei Fotoapparaten (vgl. Goodman, S. 27), welche die real auftretenden Verzerrungen ausgleichen. Bei der Mehrfluchtpunktkonstruktion ergibt sich jedenfalls ein störender „Knick“, den man zwar für die Überecksetzung des Gegenstandes benötigt, der aber in allen anderen Fällen äußerst ungewöhnlich anmutet. Vom Sonderfall des Schielens einmal abgesehen wird ein Betrachter auch nie auf zwei Blickpunkte eines Bildes gleichzeitig blicken. Es stellt sich also die Frage, wie hier selbst die hypothetische ideale Betrachtung eines Bildes mit zwei Zentren möglich wäre. Noch größer werden die Verzerrungen bei den Übergängen, wenn man gar drei oder vier Fluchtpunkte verwendet. Dies wäre unweigerlich nötig, um entgegen Goodmans Kritik auch z. B. Telegraphenmasten in den Raum hin konvergieren zu lassen.

Eine der in dieser Hinsicht glücklichsten Lösungen hat der Mathematiker und Künstler Maurits Cornelis Escher seinerzeit für seine Lithographie „Oben und Unten“ entwickelt: Um auch Höhen und Tiefenlinien konvergieren zu lassen, führte Escher neben den für die Übereckstellung erforderlichen zwei Fluchtpunkten der Ebene auch noch zwei weitere für Höhen-, und Tiefenlinien ein. Diese nennt Escher „Zenit“ und „Nadir“. Bedeutender an seiner Konstruktion ist aber vielleicht noch etwas anderes: Escher verwendet bei seiner Perspektivenkonstruktion mit vier Fluchtpunkten keine Geraden mehr, sondern gebogene Linien, um den oben angesprochenen „Knick“ beim Übergang der Bezugsysteme, der sich bei mehreren Fluchtpunkten zur Mitte hin ergeben, abzumildern bzw. zu vermeiden. Damit bügelt er – vielleicht unwissentlich – gleich noch einen weiteren Fehler der klassischen Perspektive aus: Die Annahme von Geraden als Fluchtpunktlinien. Diese ergibt sich aus zwar aus dem Modell der Projektionspyramide (die ja aus geraden Kanten aufgebaut ist), ist aber wie auch das Modell der Pyramide selbst falsch. Optisch korrekter wäre das Modell eines „Sehstrahlenkegels“ mit gewölbter Grundfläche. Dies wäre korrekter, weil das menschliche Auge, verursacht durch die Wölbung der Netzhaut, Geraden als gebogene Linien wahrnimmt. Somit kommt Eschers erweiterte Perspektive der optischen Funktionsweise des Auges schon sehr nahe. Damit soll allerdings nicht schon gesagt sein, dass die Wahrnehmung von Linien oder die Art und Weise, wie Bilder auf der Netzhaut entstehen, für die Raumwahrnehmung selbst eine Rolle spielen, auch wenn diese Vermutung jetzt sehr nahe läge.

5. Die Sache mit den Linien…

Nachdem wir in Kapitel 4 eine größere Anzahl von Raumkonstruktionen kennengelernt haben, und dabei auch immer wieder gesehen haben, wie komplex sie versuchen, der Wirklichkeit zumindest nahe zu kommen, scheint die Beweislast gegen Goodman langsam erdrückend genug, um vielleicht mittels eines Fotos einen letzten Todesstoß gegen seine Behauptung zu unternehmen, die Perspektive beruhe auf Konvention und nicht auf Ähnlichkeit.

Symmetrien des Taj Mahal (Foto: Bhavitya Indora via Pexels)

Denn ein Foto wie das obige scheint doch tatsächlich die Regeln der Perspektive zu bestätigen: Wir sehen hier Linien, die gemäß den Regeln der Perspektive gegen einen Fluchtpunkt zusammenlaufen; deutlich sichtbar, und abgesegnet durch das objektive Instrumentarium des Fotoapparates.

Doch hier sehe ich schon wieder einen Nelson Goodman hämisch grinsen. Er würde uns wohl an dieser Stelle heftig darauf hinweisen, dass erstens auch Fotoapparate nach den Regelungen unserer Sehkonvention hin konstruiert sind. Dies ließe sich vielleicht dadurch noch entkräften, das man eine Lochkamera ohne Linse (also eine fotografische ‚Camera Obscura‘) zur Aufnahme verwendet und höchstwahrscheinlich immer noch zu einem sehr ähnlichen Ergebnis gelangen würde. Weiter könnte Goodman aber unbestreitbar damit punkten, dass auf dem Foto in jedem Fall eigentlich gar keine Linien zu sehen sind.

Auf unseren Einwand hin, dass die Objekte auf dem Foto die Linien bilden, die unweigerlich auf einen Fluchtpunkt hin konvergieren, der sich irgendwo im ersten Stockwerk des Taj Mahal befindet, wird er zurecht darauf hinweisen, dass das Foto selbst aber keine Linien zeigt, sondern nur farbige (bzw. graue) Flächen. Bei Linien handelt es sich um die gedachte geometrische Verbindung von zwei Punkten auf einer Ebene. Linien selbst haben aber keine Fläche – sie sind ein eindimensionales, gedanklich-mathematisches Konstrukt. Selbiges gilt natürlich auch für die „gebogene Linien“ von Eschers erweiterter Perspektive, wie er sie in „Oben und unten“ einsetzt. Dieser Einwand gegen unsere Konvention, Fläche in Linien zu zerlegen, ist ein nicht minder harter Schlag gegen die Perspektivenlehre. Schließlich läuft daraufhin auch der Netzrahmen hinaus, der versucht, Raum auf eine Fläche zu projizieren und anschließend geometrisch zu zerlegen.

Wenn es Linien in der Wirklichkeit aber gar nicht gibt, und sie nur von uns gedacht werden, haben wir es einmal mehr nicht mit den realen Gegenständen, sondern mit „visuellen Begriffen“ derselben zu tun: Die Linien umreißen das von uns gemeinte Objekt. Sie geben die abstrakte Kontur vor, die den Begriff von allen anderen möglichen trennt. Und auch die neutrale Fototechnik wird uns da wohl nicht weiter helfen können, „denn auch die schärfste Fotografie ist nur eine Interpretation dessen, was die Kamera sieht“, wie Goodman einwendet (vgl. Goodman, S. 26) – Nicht die schärfste Fotografie, sondern die Deutung desselben, müsste man eigentlich verbessern. Denn es ist ja der Betrachter – und nicht etwa die unbelebte Fotografie – der das, was die Kamera gesehen hat, interpretiert. Nicht mechanische Apparaturen, sondern wir sind es selbst, die betrachten und deuten.

Das trifft natürlich gleichermaßen für die Wahrnehmung unserer Außenwelt wie auch die von künstlichen Bildern zu. Der Unterschied zwischen beiden besteht aber vielleicht darin, dass wir, wie Nelson Goodman immer wieder betont, unsere Außenwelt eben nicht als Fläche wahrnehmen, sondern als Raum. Daher ist ein noch so perspektivisch-getreues Bild niemals eine Abbildung der Realität, sondern bereits selbst eine geometrische Ausdeutung derselben, die Realität lediglich unseren Denkgewohnheiten gemäß exemplifiziert: eben eine Repräsentation. Zudem legt ein Bild durch seine Perspektive auch immer unweigerlich die Art und Weise, in der wir die Linien dazu denken müssen, fest. Wir können die Linien nicht einfach anders konstruieren, sonst wirkt die Perspektive falsch – der Code gibt keinen Sinn mehr. Hier greift dann auch Goodmans Argument wieder, dass man Raum also nicht realiter auf Fläche abbilden kann, und daher zwangsläufig repräsentiert.

Der Einwand all derer, die dann Goodman noch entgegen halten, dass die Perspektivenlehre zumindest doch den Versuch unternimmt, der Realität möglichst nahe zu kommen, wird Goodman nicht gelten lassen. Gegenüber allem Idealismus bleibt Goodman hier Pragmatiker. Das Ideal der Ähnlichkeit kümmert ihn nicht. Ihm geht es vielmehr darum, zu zeigen, dass die Perspektive realiter, und nicht etwa von ihrer Zielsetzung her, nicht Ähnlichkeit herstellt, sondern konventionelle Bilder konstruiert.

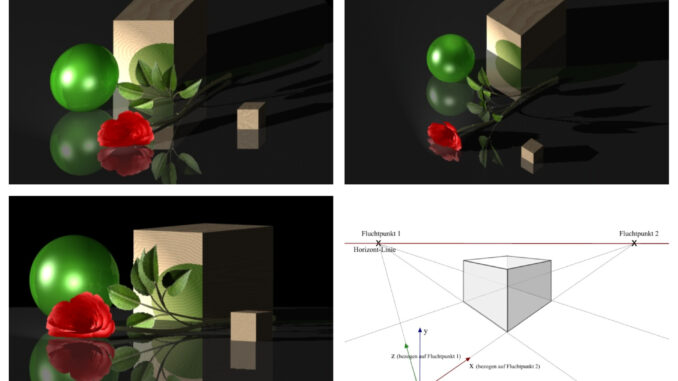
Konventionell sind die Bilder auf zweierlei Weise: Erstens konotiert Perspektive Räumlichkeit in einer vereinbarten Weise (also konventionell) auf Fläche. Sie ist dabei keineswegs die einzige Möglichkeit. Bislang wurde hier auch völlig ausgespart, dass dabei fast immer noch Farbe und Schattierung zum Einsatz kommt. Diese beiden Komponenten tragen überdies meist viel mehr zum Realismus eines Bildes bei als seine zugrundeliegende Linienstruktur, ja sie ist sogar zwingend erforderlich, um ein Bild erst „realistisch“ zu machen. Tatsächlich scheinen Bilder mit fotografischer Farbstruktur sogar dann realistisch, wenn die Perspektive nicht stimmt, wie folgenes Beispiel zeigt:

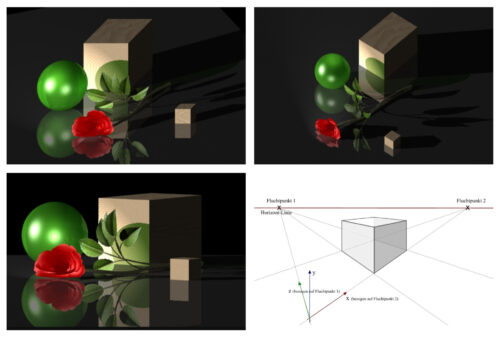
Die drei Computergrafiken meiner Beispielabbildung sind „fotorealistisch“, könnten also ohne weiteres für Fotografien gehalten werden, die von den Objekten aus verschiedenen Blickwinkeln aufgenommen wurden. Tatsächlich handelt es sich bei allen dreien aber um „Computerfiktionen“, die vom Computer unter Zuhilfenahme der drei Konstruktionsmethoden Parallelprojektion, Isometrie und Zweifluchpunktperspektive errechnet wurden. Trotz der unterschiedlich perfekten geometrischen Konstruktionen erscheinen alle – jede für sich – realistisch, weil sie ziemlich perfekt die Fläche, hier die Fläche eines Fotos, nachbilden, also unserer Konvention für Foto entsprechen. Es wäre natürlich auch denkbar, den Computer bzw. im Idealfall den Künstler anzuweisen, ein anderes System zur Flächenwiedergabe, z. B. ein Ölgemälde zu konstruieren. Dass dies dem heutigen Betrachter nicht so real erscheint wie eine Fotografie, müsste man gemäß Goodman auf Gewohnheit zurückführen.

Interessant ist hier auch, dass die meisten gebräuchlichen Raytracing-Systeme, die realistische Computergrafiken erzeugen, nicht etwa den Anspruch erheben, originalgetreu die Realität selbst wiederzugeben, sondern lediglich, „fotorealistisch“ zu sein. Zum Ideal wird hier also das Medium Foto erklärt, und nicht etwa der reale Raum selbst. Dieser ist nur noch indirekt als Szene in der Grafik vertreten. Es ist aber gerade auch nicht das Ziel von Computerkünstlern, Grafiken zu erstellen, die man für Fotos hält, sondern nur welche, die aussehen, als ob sie Fotos sein könnten. Sofern es sich um schlichte Replikate handeln würde, wäre der eigentliche Reiz der Computergrafik ja dahin. Von Produzenten von Fakenews abgesehen legen daher die meisten Computergrafiker großen Wert darauf, dass man den Kunstcharakter ihrer Werke erkennt.

Gegenüber dem Medium Computergrafik erhebt die Perspektive aber durchaus nicht nur den Anspruch, „fotorealistisch“ zu sein. Sie will nicht nur einem bestimmten Medium ähnlich sein, sondern dem Gegenstand, den sie jeweils repräsentiert, selbst. Daran nun aber stößt sich Goodman: Eine Fläche ist dem Raum niemals ähnlich, und selbst wenn es so wäre, wäre das nicht der entscheidende Punkt. Entscheidend ist, so Goodman, dass ein perspektivisches Bild seinen Inhalt angemessen repräsentiert. Dazu ist ausgesprochene Ähnlichkeit weder unbedingt notwendig, noch immer unbedingt nützlich. Viel wichtiger ist, dass der repräsentierte Inhalt vom Betrachter gut denotiert werden kann. Wenn also Perspektive wirklich nicht in erster Linie auf Ähnlichkeit basiert, warum ist es ihren Vertretern dann offensichtlich trotzdem so wichtig, auf der Ähnlichkeit zu bestehen?

Vielleicht handelt es sich dabei gar nicht so sehr um eine technische als vielmehr eine erkenntnistheoretische Frage: Es geht wieder mal um die Frage nach der Wahrheit. Perspektive ist nämlich noch auf eine zweite Weise konventionell: Gerade die Linienperspektive projiziert nämlich auch Räumlichkeit in die Begrifflichkeit der Geometrie: Sie deutet Raum geometrisch aus. Dabei beschränkt sie sich, wie der Netzrahmen deutlich macht, keinesfalls auf das Medium Bild, sondern sie deutet selbst die im Bild behandelte Wirklichkeitswahrnehmung geometrisch/perspektivisch aus. Perspektive ist damit nicht mehr nur eine Konvention zur Darstellung von Raum auf Flächen, sondern ein Instrument zur Deutung der uns umgebenen Wirklichkeit als geometrisches Regelsystem. Im Sinne der klassischen Zentralperspektive handelt es sich bei Raum nicht nur um einen dezentrales Fluidum, in dem die Objekte als visuelle Begriffklötze unabhängig voneinander irgendwie existieren, sondern um einen zielgerichteten Erfahrungsraum mit einem logisch strukturierten Zentrum, der im Fluchtpunkt endet, aber letztlich nicht von ihm – sondern vom betrachtenden Subjekt her konzipiert ist, das seinen Blick in den Raum richtet.

Dies ist die eigentliche zentrale Bedeutung der Perspektive: Der Mensch ist Mittelpunkt eines von ihm aus betrachteten, logisch-mathematisch strukturierten Universums. Der Betrachter durchdringt diese Struktur: Er hat den Durchblick.

6. Sinn und Zweck von Blickrichtungen

Die Perspektive repliziert nicht die Wirklichkeit, sie ist ein Instrument, das in erster Linie dem Betrachter dient. Erwin Panofsky beginnt seinen 1997 erschienen Essay „Perspective as Symbolic Form“ folgerichtig mit einem Zitat von Albrecht Dürer, einem der Wegbereiter der Zentralperspektive: „Item Perspectiva ist ein lateinisch Wort, bedeutet Durchsehung“. Perspektive stellt ein Instrumentarium dar, durch das ich blicken muss, um die Welt zu erkennen. Als Konstruktionshilfe empfielt er den sogenannten „Netzrahmen“.

Zum Sehen allein brauche ich den Netzrahmen nicht, sondern nur meine Augen. Es wurden auch schon vor der „Entdeckung“ der Zentralperspektive in der Renaissance eine ganze Menge Gemälde gemalt. Der Netzrahmen und das System der Perspektive dienen vielmehr als Deutapparat für das Gesehene: Das Gesehene wird in einem ganz bestimmten Blickwinkel betrachtet und zu diesem hin aufgeschlüsselt. Wenn der Netzrahmen beispielsweise Landschaft in Linien und Koordinaten zerlegt, so gibt mir die Perspektive bei der Rezeption als „gedachter Netzrahmen“ die Sehnormen an die Hand, wie ich Welt geometrisch in Sinn stellen kann. Die Perspektive ist somit Anleitung zur Betrachtung. Sie stellt aber keinen natürlicher Sehvorgang dar, wie oft angenommen. Menschliche Optik und Lineare Geometrie sind nur bedingt kompatibel, wenn auch nicht unvereinbar. Andererseits ergeben Lichtstrahlen an sich wirklich auch noch keinen Sinn. Sie müssen nach irgendeinem einem Code verarbeitet werden. Nötig ist immer eine Ausdeutung des Gesehenen.

Die Betrachtungsweise der Perspektive stellt keineswegs die ultimative und einzige Möglichkeit der kognitiven Bildverarbeitung dar. Sie ist auch mitnichten neutral und selbstverständlich, sondern historisch, wie Panofsky gezeigt hat, und impliziert ein bestimmtes Welt,- und auch Menschenbild. So verlangt die Zentralperspektive das neuzeitliche Individuum, welches Welt in seinem ganz eigenen Sinne zielgerichtet und von sich aus betrachtet. Andere Formen, wie Bedeutungsperspektive, welche ein geometrisches System nicht vom Betrachter aus, sondern umgekehrt von zentralen Objekten des Bildes darstellen, sind nicht nur denkbar, wie Goodman argumentiert, sondern in der Kunstgeschichte auch tatsächlich nachweisbar. Ein bekanntes Beispiel wäre die Ikonografie, die religiöse Inhalte (Heilsräume) von ihrer Bedeutsamkeit her repräsentiert.

Man muss Blickrichtungen auch nicht unbedingt zwingend vorschreiben, um geometrische Räume zu erzeugen: So stellt die Parallelprojektion (geometrische) Körper als vollkommen unschuldige und neutral zu betrachtete Gegenstände dar: Wie viele Würfel man auch nebeneinander setzt, alle erscheinen aus derselben undefinierbaren Idealansicht. Räumlichkeit ist hier betont repräsentativ, damit aber auch unglaublich informativ, weil nur das exemplifiziert wird, was auch gezeigt werden soll. Die Isometrie ist in dieser Hinsicht tatsächlich schon eher ein Zugeständnis an unsere optische Wahrnehmung, aber auch sie betrachtet ihre Objekte nicht natürlich, sondern von einer postulierten Idealperspektive aus, die gleichermaßen für alle dargestellten Objekte gleich gilt. Parallelprojektion wie auch Isometrie erzeugen betont keine zu große Ähnlichkeit mit der Natur, sondern Anschaulichkeit und Überblick, der bei einer allzu natürlichen Darstellung nur verloren ginge.

Schließlich kann man Raum auch durch das bloße Übereinanderstapeln von Objekten erzeugen, oder ganz auf räumliche Bezugnahme verzichten, dennoch aber Raum, z. B. Landschaft, mit Flächen realisieren. Alle Bilder bestehen natürlich aus Flächen. Aber selbst ohne geometrisches Grundraster können die Flächen, z. B. durch die klassische Farbenlehre, Raum erzeugen. Letztlich kommt dies der natürlichen Wahrnehmung sogar noch am nächsten. Denn in natura sehen wir ja selten Quader ordentlich in einer Schachbrettlandschaft stehen. Die Natur ist vielmehr das Chaos von scheinbar oder tatsächlich bezugslosen Gegenständen, die ich selbst aber nur als Farben wahrnehme. Den Gegenstand als solchen wahrzunehmen, ihn mit einer sozusagen „kognitiven Kontur“ zu umgeben, ist schließlich schon wieder seine Deutung. Was auch einer der Gründe ist, dass selbst moderne KI-Ansätze an Zeichnungen oft noch scheitern, da es ihnen am dafür nötigen Weltwissen fehlt. Zeichnen ist harte Denkarbeit: gekonnte Abstraktion. Sie ist in hohem Maße „künstlich“.

Vielleicht versuchten die Maler nach der Renaissance bis zum Impressionismus deshalb, grobe Linien und Konturen tunlichst zu vermeiden, weil dadurch die Illusion, man habe es mit unschuldiger Abbildung zu tun, im Keim erstickt worden wäre. Die Künstler versuchten also immer wieder, ihre Technik, und damit auch den Deutungscode, zu verbergen. Dies ist nicht unbedingt ein Widerspruch zu Goodmans Symboltheorie, die auf kodierter Repräsentation basiert, und damit auf den Code angewiesen ist; und es widerspricht auch nicht der Perspektivenlehre selbst, wenn man sie zu vertuschen sucht: Denn ein perspektivisches Gemälde muss die Linien, nach denen es gemalt ist, nicht offen gestehen. Es genügt vollkommen, dass der geschulte und suchende Betrachter sie sich ungestört hineindenken kann.

Der Unterschied zwischen dem „Bild“ und der realen Wahrnehmung besteht darin, dass ein Bild sein Deutungsmuster bereits vorgibt, es ist bedeutungsmässig „vorgekaut“. Demgegenüber ist die Realität an und für sich sinneutral- auch wenn es das Auge ihres Betrachters nicht ist. Man kann reale Landschaft durchaus mit gewisser Berechtigung als zentralperspektivische Weltlandschaft, als mittelalterliche Zeichenlandschaft, als pointillistische Impression oder als absurdes Chaos betrachten, sofern man darauf geschult ist. Ästhetik ist mit Erkenntnis durchaus kompatibel. Davon lebt letztlich auch die Fremdenverkehrsindustrie.

Allerdings sollte man doch der Realität mitunter ein mehr an Inhalt zugestehen, ein gewisses Moment des Unnahbaren. Welche Art der Wahrnehmungskonvention man auch wählt, die Realität bleibt letztlich immer unerreicht. Missachtet man dies, kann es einem sonst durchaus geschehen, dass man während seiner ästhetischen Betrachtungen in einen Teich der Realität stolpert (wie dies in Wilhelm Buschs Zeichengeschichte „Plisch und Plum“ Herrn Pief passiert, der die Welt immer nur durch sein „Perspektiv“ (Fernglas) sehen will – man scheitert dann an der Realität, obwohl man doch ein scheinbar so objektives Sehinstrument benutzt hat, mit dem man weiter blicken konnte als ohne. Einen ähnlichen Fall stellt Max Frisch in seinem Werk „Homo Faber“ vor, in dem der technikaffine Protagonist Walter Faber in seinen Versuchen scheitert, die chaotische Wirklichkeit durch seine Videokamera zu objektivieren (und damit unter Kontrolle zu bekommen). Man ist zum Scheitern verurteilt, wenn man annimmt, technische Hilfsmittel allein würden das chaotische Element der Wirklichkeit auflösen.

7. Escher oder der „Knick in der Optik“

Dass dies auch in Sachen Perspektive möglich ist – noch dazu trotz seiner wesentlich verbesserten Konstruktionsmethoden, zeigt Maurits Cornelis Escher immer wieder mit seinen Lithographien. Escher präsentiert dem Betrachter geometrisch (und teilweise) auch optisch stimmige Szenarien, die dennoch unserem gesunden Menschenverstand widersprechen. Wäre es Realität, müssten wir eine Art Zauberei annehmen, oder wir würden seine Grafiken einfach nicht verstehen. Da wir aber durchaus erkennen, dass es sich jeweils lediglich um Bilder handelt, können wir uns nur wundern. Dabei geht es Escher aber gerade nicht darum, uns das Unmögliche plausibel zu machen, etwa in der Weise, wie es noch im 19. Jahrhundert Mode war, wenn findige Scharlatane allerlei Fabeltiere aus Tierkadavern zusammennähten und dem schaulustigen Publikum als reale Artefakte präsentierten. Escher zeigt seinen Zuschauern vielmehr bewusst eine Illusion, von der alle Wissen sollen, dass es eine Illusion ist; und dazu benötigt er die von Goodman konstatierte Distanz zwischen der Wahrnehmungskonvention der Optik/Geometrie und der Realität. Folglich täuscht nicht Escher die Betrachter, sondern die Betrachter täuschen sich selbst mittels ihrer für absolut gehaltenen Sehkonvention.

Bilder sind in dem Sinne, wie sie strukturierte Information vermitteln, immer auch bis zu einem gewissen grade Behauptungen, Hypothesen. Solange man eine Behauptung aber als solche erkennt, muss man sie nicht automatisch für bare Münze nehmen: Man kann sie kritisieren. Die Möglichkeit zur Kritik basiert darin, dass man erstens eine Behauptung als solche erkennt, zweitens ihre zugrundeliegende Struktur durchschaut und sie drittens nicht für absolut hält. Eine Kritik wäre ja sonst „undenkbar“.

Eschers Bilder wirken nun so entsetzlich, weil wir sie zwar als Behauptung erkennen (weil sie etwas behaupten, was undenkbar ist), und weil wir auch wissen, wie sie aufgebaut sind (wir erkennen ihre Konstruktion). Aber dieses Konstruktionssystem halten wir für so absolut, dass wir uns nur wundern können, wie es sein kann, dass etwas dem realistischen System der Perspektive entspricht und dennoch offensichtlich irreal ist. Da „trauen wir unseren Augen nicht“ – Aber daran liegt es gar nicht, denn die Optik ist korrekt. Was nicht stimmig ist, ist nicht etwa die Konstruktion, sondern ihr Absolutheitsanspruch bei der Vermittlung von objektiver Realität.

Nicht alles, was wir sehen, ist real. Das ist das Funktionsprinzip von optischen Täuschungen. Aber Eschers Zeichnungen sind nicht nur optische Täuschungen, sie sind oft auch gerade perspektivische Täuschungen: Escher zeigt beispielsweise, dass auch Perspektive und die Geometrie nicht eins sind. Dies ist das Funktionsprinzip der „unmöglichen Lattenkiste“, wie sie beispielsweise in der Lithographie „Beveldere“ von 1958 eingesetzt wird, oder auch bei „Treppauf und Treppab“ (1960), oder „Wasserfall“ (1961), die beide real unmögliche Rekursionen perspektivisch plausibel darstellen. Bei „Oben und Unten“ macht sich Escher hingegen zunutze, dass es nach den Regeln der Perspektive wie der Optik völlig irrelevant ist, welcher Fluchtpunkt oben (Zenith) und welcher unten (Nadir) ist. In der Realität würde hier die Schwerkraft und ihren Tribut fordern. Diese wird aber von beiden Repräsentationssystem nicht exemplifiziert. Beide Systeme sind nicht absolut, und umfassen daher nicht die gesamte Realität.

Insofern kann man den eingangs erwähnten Widerspruch, was den Stellenwert von Perspektive in Wissenschaft (bzw. Sprache) und Kunst (bzw. Bild) angeht, wie folgt auflösen:

Die Perspektive ist offensichtlich auch in der Kunst nicht das unabdingbare Instrument, um Realität „korrekt“ wiederzugeben. Sie ist lediglich ein System der Repräsentation, um bestimmte Eigenschaften von realen Gegenständen visuell zu repräsentieren. Sie repräsentiert ihrem zugrunde liegenden System entsprechend Realität als räumlich-geometrische Struktur. Damit reproduziert sich sich letztlich lediglich selbst.
Gerade darin liegt aber auch vielleicht auch ihre Stärke: Denn als Repräsentationssystem kann Perspektive auch als Instrument dazu verwendet werden, die Realität sinnvoll zu deuten. Damit ermöglicht sie vielleicht auch, innerhalb ihrer Systemgrenzen, deutlicher und weiter zu sehen, ja überhaupt etwas zu erkennen. Sicherlich gibt es sonst kaum ein visuelles System, welches die Realität in ihrer Eigenschaft als geometrische Struktur so angemessen zum Ausdruck bringt.
Gegenüber fortgeschritteneren Systemen der Optik, wie beispielsweise der Fotografie, muss man die Perspektive allerdings auch hier in ihre Schranken verweisen. Selbst dem Versuch einer Verbesserung von Perpektive in Richtung Optik (wie es z. B. die „Schattenperspektive“ versucht), muss man entgegenhalten, dass sie der Realität damit nicht näher kommen würde als das System der Fotografie selbst: Im besten Falle hätten wir es mit „fotorealistischen“ Bildern zu tun, aber nicht mit direkter Abbildung der Realität.

Die Grenzen werden hier vom System wie auch vom Medium der Fläche vorgegeben. Das derzeit optimale optische System ist und bleibt aber das menschliche Auge; solange es als Rezeptionsorgan nicht ersetzt wird, wird sich daran wohl auch nichts ändern; gegenüber Fotografie und Flächenperspektive hat es nämlich den Vorteil, wirklich räumlich zu sehen, und nicht nur Raum auf Fläche repräsentieren zu müssen. Begrenzt ist allerdings auch dieses System. Weshalb hätte man sonst erst versuchen sollen, es durch allerlei künstliche Apparaturen zu ersetzen, um damit weiter zu sehen?

8. Weiterführende Literatur

Bärtschi, Willy A.: Geometrische Linear- und Schattenperspektiven: Geschichte, Konstruktionsanleitung und Erscheinungsformen in Umwelt und bildender Kunst. Wiesbaden, 1994.
Birkhofer, Gerhard: Die Perspektivische Darstellung. (ALS-Arbeitsmappe). Dietzenbach, 1995.
Bögeholz, Harald/Stieler, Dr. Wolfgang: Vom Röhrenmonitor zum 3D-Interface. In: c’t, 1999, Nr. 6, S. 180.
Busch, Wilhelm: Plisch und Plum. In: Das Große Wilhelm Busch Buch. Niedernhausen, 1997.
Ernst, Bruno: Der Zauberspiegel des Maurits Cornelis Escher. Köln, 1994.
Goodman, Nelson: Sprachen der Kunst, Entwurf einer Symboltheorie. Frankfurt a. M., 1998.
Panofsky, Erwin: Perspective as Symbolic Form. New York, 1997.
Parramón, José M.: comment dessiner en perspective. Paris, 1972.
Wiegerlin, Klaus: Medienethik. Stuttgart, 1998.